- Momen Gaya
Perhatikan gambar berikut ini!
F : Gaya
(N)
O
: Pusat massa benda/pusat momen
ℓ : Jarak antara garis kerja gaya dengan pusat massa benda. (m)
Pehatikan gambar 9.4 (a) Gaya
F yang garis kerjanya mengenai pusat massa benda (O) membuat benda bergerak Translasi.(bergeser),
Sedangkan pada gambr 9.4 (b) Gaya
F yang garis kerjanya mempunyai jarak tertentu (ℓ) dari pusat massa benda (O)
dan menyebabkan benda menjadi berotasi disebut momen gaya/torsi.
Persamaan
momen gaya adalah sebagai berikut!
Keterangan
:
r : Vektor
kedudukan (m)
F :
Gaya (N)
Keterangan :
l
F :
Gaya (N)
I
Jika antara sudut r dan F adalah
, maka besar momen gaya adalah :
Arah Momen Gaya
Arah Momen Gaya
Momen
gaya merupakan besaran Vektor, Arah
momen Gaya di tentukan sebagai berikut:
1. Dengan menggunakan aturan tangan
kanan perhatikan gambar 9.6
Telapak tangan dengan 4 jari mengepal, arah 4 jari
menunjukkan arah gaya (F), sedangkan arah jempol menunjuk keatas menunjukkan
arah momen gaya.
2. Arah Momen gaya juga
dapat dinyatakan menurut arah gaya
Perhatikan gambar 9.7 diatas besar gaya (F) yang bekerja
berjarak r terhadap pusat massa (P), momen gaya bernilai positif jika arah
searah jarum jam, dan sebaliknya berharga negatif jika berkebalikan dengan arah
jarum jam
Resultan beberapa Momen
Gaya
Perhatikan gambar 9.8 diatas terdapat 4 buah momen gaya
yang bekerja pada sistem, untuk itu resultan momen gaya adalah jumlah dari ke 4
momen gaya
Jadi resultan momen gaya adalah:
Momentum Sudut (ANGULER)
Partikel yang bergerak melingkar
memiliki momentum sudut. Untuk memahami hal ini, bayangkan sebuah partikel
bermassa
berputar dengan kecepatan sudut
pada suatu sumbu putar
yang terletak pada jarak
dari partikel itu. Lalu linear partikel itu
adalah
dan nilai momentum linear partikel itu adalah:
Dalam gerak rotasi, yang dimaksud
momentum sudut (anguler) adalah momen momentum linear terhadap suatu sumbu
putaran. Jika momentum sudut kita beri lambang
, untuk itu momen sudut merupaka perkalian momen p linier terhadap jarak r:
Dengan memasukkan persamaan p= m v sehingga menjadi:
Karena
dan
merupakan besaran
vector,
dan
merupakan hasil perkalian dua vektor
(perkalian silang), antara
vektor
dan vektor
. Momentum Sudut dirumuskan :
Jika sudut antara
dan
adalah
, maka besar momentum sudut
kita nyatakan:
Arah
momentum sudut ditentukan dengan aturan tangan kanan, seperti penentuan arah
momen gaya. Lipatlah keempat jari dari arah
ke
, maka ibu jari menunjukkan arah
.
Resultan Momentum sudut
Benda
selalu dipandang terdiri atas banyak partikel dengan massa
dan seterusnya. jarak masing-masing partikel
dari sumbu putaran
dan seterusnya. Semua partikel berputar dengan
kecepatan sudut sama, yaitu
. Jadi, momentum sudut
masing-masing partikel dapat kita tuliskan:
dan seterusnya. Formulasi untuk resultan momen sudut adalah:
Momen Inersia
Besaran massa terhadap kuadrat jarak sumbu
putar sangat penting artinya untuk menganalisis sifat gerak berputar. Pada gerak translasi sifat kelembaman direpresentasikan
dengan massa, dalam gerak rotasi kelembaman di representasikan dengan I, Besaran
ini kemudian disebut momen inersia. Sebuah
partikel bermassa
yang berputar pada sebuah sumbu berjarak
dari
, dikatakan memiliki momen inersia
sebesar:
Momen inersia merupakan besaran
skalar. Satuannya dalam SI ialah
. Untuk momen inersia sebuah benda
terhadap suatu sumbu putar, dapat dipandang sebagai jumlah momen inersia
partikel-partikel penyusunannya.
Momentum sudut dan
momen inersia
Telah kita bahas
diatas bahwa persamaan momen sudut
, sedangkan persamaan momen inersia dinyatakan bahwa
. Tugas kita berikutnya adalah mencoba memhubungkan kedua
persamaan, dengan memperhatikan bahwa I=mr2, dan
,kita akan diperoleh:
Perhatikan persamaan
momentum sudut
di atas, tampak mirip (analog) dengan
persamaan momentum linier
. Analogi ini menunjukkan gerak translasi dan gerak rotasi mereka identik!
Beberapa Kasus Dalam
Menentukan Momen
Inersia
Besarnya
momen inersia beberapa
bentuk benda dapat kita tentukan melalui
perhitungan matematis. Ternyata besarnya
momen inersia suatu benda bergantung pada bentuk benda dan letak sumbu
putarnya. Berikut ini akan kita cari Momen inersia beberapa benda
Pada batang silinder pejal dengan sumbu melalui pusat dapat kita tentukan
melalui berikut ini!
I = mr2
I = mr2
Momen
gaya dan percepatan sudut
Misalkan sebuah silinder dipengaruhi oleh sebuah gaya tetap
yang arahnya
menyinggung permukaan silinder. Gaya
ini menimbulkan momen
gaya sebesar
dan memberikan percepatan sudut (perubahan kecepatan
sudut) pada silinder.
Menurut
hukum II Newton,
, maka kita dapat
menuliskan hubungan:
Hubungan
percepatan linear
dengan percepatan sudut (anguler)
adalah
.
Dengan demikian,persamaan
menjadi:
Sudah
kita ketahui bahwa harga
itu adalah momen inersia
Oleh karena
itu,persamaan
dapat
kita tulis menjadi :
Persamaan
tersebut tampak menyerupai (analog) dengan persamaan
(Hukum II Newton).
Energi Kinetik Rotasi dan Translasi
Dalam
gerak translasi, kita telah mengenal energi kinetik translasi, dengan rumusan:
Dalam
gerak rotasi pun kita akan berhubungan dengan energi kinetik rotasi, yang
dirumuskan sebagai:
Keseimbangan benda tegar
Pada kasus sehari-hari umumnya
suatu benda bergerak mengalami gerak translasi dan rotasi. Bila benda
tidak bertranslasi tetapi hanya berotasi dikatakan benda itu memiliki
keseimbangan translasi Persyarat keseimbangan translasi adalah (untuk 2 dimensi)
∑ F= 0 →
∑ Fx=0
∑ Fy=0
benda
yang memikili keadaan diatas dikatakan tidak mempunyai percepatan linear, dalam arti a (percepatan) adalah 0,
benda ini mungkin dalam keadaan :
1.
diam ( seimbang statis) atau
2. bergerak dengan kecepatan tetap (
seimbang dinamis)
Sebaliknya
suatu benda memiliki keseimbangan rotasi apabila benda tersebut tidak memiliki
percepatan sudut atau
adalah 0
, benda ini mungkin :
1. diam
2. memiliki kecepatan sudut tetap (ω)
Apabila suatu benda sekaligus memiliki kedua keseimbangan,
transslasi dan rotasi maka benda tersebut memerlukan syarat :
∑ F = 0
∑
= 0
Hubungan Antara Gerak Translasi dan Rotasi.
Titik Berat benda
Jika kita memperhatikan sebuah benda maka dapat kita
anggap bahwa benda ini merupakan kumpulan titik-titik materi yang padanya
bekerja gaya-gaya berat, gaya berat ini menuju pusat bumi dan tegak lurus ke
permukaan bumi titik tangkap gaya berat benda itu disebut titik berat.
Untuk benda
yang bentuknya teratur, misalnya balok atau kubus titik beratnya terletak di perpotongan diagonal ruang bangun
tersebut.
Untuk benda
yang tidak teratur misal sebuah kertas karton untuk menentukan titik beratnya
adalah :
1. Buat
lubang di tepi karton dan gantung benda tersebut dengan benang, buatlah tanda garis mengikuti garis tegak lurus
benang.
2. Buat lah
lubang lagi di tepi karton sembarang dan lakukan seperti no.1, kemudian
tentukan garis perpotongan garis tadi. Ini adalah pusat massa dari karton.
Untuk benda gabungan yang bentuknya teratur perumusanya adalah:
Untuk benda gabungan yang bentuknya teratur perumusanya adalah:
Macam –macam keseimbangan
Keseimbangan Stabil adalah
keseimbangan apabila gaya dihilangkan maka dalam beberapa saat ia akan diam
kembali di tempatnya
Contoh:
kelereng di taruh di mangkuk
Keseimbangan labil adalah : keseimbangan
apabila gaya dihilangkan maka dalam beberapa saat ia tidak akan kembali di tempatnya
Contoh :
kelereng di taruh diatas bola
Keseimbangan netral (indiferent)
adalah: keseimbangan apabila gaya dihilangkan maka ia akan diam tetapi di
tempat yang berbeda,titik berat benda tetap pada satu garis lurus.
Contoh: kelereng di taruh
di lantai
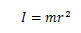
0 Response to "MATERI MOMEN GAYA"
Post a Comment