variabel yang mempengaruhi fungsi gelombang ѱ (psi) adalah variabel posisi (x) dan variabel waktu (t) :
secara matematis dituliskan :
Ѱ(x,t) (1)
kemudian konjugat dari fungsi gelombang tersebut adalah :
Ѱ*(x,t) (2)
konjugate secara matematis berkebalikan tanda dengan dengan nilai imajiner i ; (ѱ jika direpresentasikan ke fungsi complex number ѱ = x + iy), jadi Ѱ* adalah x - iy
dengan psi adalah fungsi propabilitas. dan menggunakan distribusi kontinu dari ilmu statistik sehingga normalization:
 (3)
ini adalah interprestasi statistik dari sebuah fungsi gelombang. kita mengintegralkan dari negatif tak hingga sampai tak hingga absolut psi hasil nya adalah1 atau kita mengintegralkan dari negatif tak hingga sampai tak hingga psi konjugate psi diperoleh nilai 1,
(3)
ini adalah interprestasi statistik dari sebuah fungsi gelombang. kita mengintegralkan dari negatif tak hingga sampai tak hingga absolut psi hasil nya adalah1 atau kita mengintegralkan dari negatif tak hingga sampai tak hingga psi konjugate psi diperoleh nilai 1,
kita akan mencari apakah revolusi waktu berpengaruh pada normalisasi atau tidak berpengaruh pada normalisasi;
fungsi Gelombang kita turunakan terhadap waktu
 (4)
(4)
dengan menggunakan aturan integral menjadi :
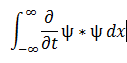 (5)
dengan defernsial partial menjadi:
(5)
dengan defernsial partial menjadi:
 (6)
persamaan Schrodinger :
(6)
persamaan Schrodinger :
 (3)
(3)kita akan mencari apakah revolusi waktu berpengaruh pada normalisasi atau tidak berpengaruh pada normalisasi;
fungsi Gelombang kita turunakan terhadap waktu
 (4)
(4)dengan menggunakan aturan integral menjadi :
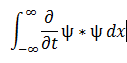 (5)
(5) (6)
(6)






0 Response to "NORMALISASI FUNGSI GELOMBANG SEBUAH PARTIKEL"
Post a Comment